Conclusión

Bueno como vimos anterior mente se hablo del cálculo diferencial e integral. Sobre los conceptos que tienen cada una y sus diferencias pro ejemplo nos dice que en el cálculo integral es lo inverso del diferencial.

Y se hablo sobres las formulas para calcular para su desarrollo de una función de una derivada, y sus reglas. Ya que da la misma manera aplicamos en la vida cotidiana por ejemplo: cuando un automóvil viaja y lleva una distancia  un tiempo y una aceleración sele llama  límite. Bueno este tema nos dimos cuanta que es importante ya que la utilizamos diariamente en nuestra vida.  

               Ejemplos para calcular su movimiento



""Crees que se mueve o solo te lo imaginas""

¿Cuantas veces pasa el circuito por el mismo punto ?

¿Calcula a que velocidad gira sobre su mismo eje y a que tiempo?

El calculo

¿Como se define el cálculo integral?

 Nos habla que El cálculo integral se basa en el proceso inverso de la derivación, llamado integración. Dada una función f, se busca otra función F tal que su derivada es F' = f; F es la integral, primitiva o anti derivada de f, lo que se escribe F(x) = f(x)dx o simplemente F = f dx (esta notación se explica más adelante).

¿Para que se utiliza las tablas de derivación?

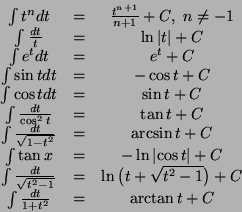Se utiliza para la forma más general de la integral de f es F + c, en donde c es una constante cualquiera llamada constante de integración; esto es debido a que la derivada de una constante es 0 por lo que (F + c)' = F' + c' = f + 0 = f.

Las reglas

Nos habla que, Las reglas básicas de integración de funciones están compuestas y son similares a las de la diferenciación. La integral de la suma (o diferencia) es igual a la suma (o diferencia) de sus integrales, y lo mismo ocurre con la multiplicación por una constante.

Teorema del cálculo integral

Éste es el teorema fundamental del cálculo, que se cumple siempre que f sea continua entre a y b, y se tenga en cuenta que el área de las regiones por debajo del eje x es negativa, pues f(x) < 0. (Continuidad significa que f(x) f(x0) si x x0, de manera que f es una curva sin ninguna interrupción).

¿Que es la función de una derivada?

La derivada dy/dx = f'(x) de una función y = f(x) puede ser diferenciada a su vez para obtener la segunda derivada, que se denota d2y/dx2, f''(x) o D2f. Si por ejemplo x es el tiempo e y es la distancia recorrida, entonces dy/dx es la velocidad v, y d2y/dx2 = dv/dx es el incremento en la velocidad, es decir, la aceleración. Según la segunda ley del movimiento del Newton, un cuerpo de masa constante m bajo la acción de una fuerza F adquiere una aceleración a tal que F = ma.

Velocidad 

                                            distancia

Ejemplos

. si el cuerpo está bajo la influencia de un campo gravitatorio F = mg (donde g es la magnitud del campo), y entonces ma = F = mg por lo que a = g, y por tanto dv/dx = g. Al integrar, se tiene que v = gx + c, en donde c es una constante; sustituyendo x = 0 se ve que c es la velocidad inicial. Integrando dy/dx = v = gx + c, se tiene que y = ½gx2 + cx + b en donde b es otra constante; sustituyendo de nuevo x = 0 se tiene que b es el valor inicial de la y

¿Como calcular la derivada de una función?

Para calcular la derivada de una función, nos dice que, hay que tener en cuenta unos cuantos detalles: primero, se debe tomar una h muy pequeña (positiva o negativa), pero siempre distinta de cero. Segundo, no toda función f tiene una derivada en todas las x0, pues k/h puede no tener un límite cuando h 0; por ejemplo, f(x) = |x| no tiene derivada en x0 = 0, pues k/h es 1 o -1 según que h > 0 o h < 0; geométricamente, la curva tiene un vértice (y por tanto no tiene tangente) en A = (0,0).

Formulas para resolver una función diferencial e integral

Aquí se representa como cuales son los 4 pasos para la derivación de una función

¿Crees que se mueven?

Si o noo00¡¡¡..

 

¿Que es el calculo diferencial?

Bueno brevemente  no s dice que: El cálculo diferencial estudia los incrementos en las variables. Sean x e y dos variables relacionadas por la ecuación y = f(x), en donde la función f expresa la dependencia del valor de y con los valores de x.

A continuación nos muestra un ejemplo que, x puede ser tiempo e y la distancia recorrida por un objeto en movimiento en el tiempo x. Un pequeño incremento h en la x, de un valor x0 a x0 + h, produce un incremento k en la y que pasa de y0 = f(x0) a y0 + k = f(x0 + h), por lo que k = f(x0 + h) - f(x0).

Después nos dice que El cociente k/h representa el incremento medio de la y cuando la x varía de x0 a x0 + h. La gráfica de la función y = f(x) es una curva en el plano xy y k/h es la pendiente de la recta AB entre los puntos A = (x0,y0) y B = (x0 + h, y0 + k) en esta curva; esto se muestra en la figura 1, en donde h = AC y k = CB, así es que k/h es la tangente del ángulo BAC.

¿Qué es un límite?

 Es definido como  un concepto que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor.

Antecedentes históricos del cálculo

¿Quienes fueron los que descubrieron en cálculo? nos dice que Demócrito calculó el volumen de pirámides y conos, se cree que considerándolos formados por un número infinito de secciones de grosor infinitesimal (infinitamente pequeño).

Antecedentes históricos del cálculo

¿Quienes fueron los que descubrieron en cálculo? nos dice que Demócrito calculó el volumen de pirámides y conos, se cree que considerándolos formados por un número infinito de secciones de grosor infinitesimal (infinitamente pequeño),

De igual manera que utilizaron el "método de agotamiento" para encontrar el área de un círculo con la exactitud requerida mediante el uso de polígonos inscritos. Sin embargo, las dificultades para trabajar con números irracionales y las paradojas de Zenón de Eleaim pidieron formular una teoría sistemática del cálculo.

En el siglo XVII, no habla Francesco B. Cavalieri y Evangelista Torricelli ampliaron el uso de los infinitesimales, y Descartes y Pierre de Fermat utilizaron el algebra para encontrar el área y las tangentes (integración y diferenciaciónen términos modernos).

Descartes

Pierre de Fermat

Otros mencionados como son Fermat e Isaac Barrow tenían la certeza de que ambos cálculos estaban relacionados, aunque fueron Isaac Newton (hacia 1660) y Gottfried W. Leibniz (hacia 1670) quienes demostraron que son inversos, lo que se conoce como teorema fundamental del cálculo.

Después ,El descubrimiento de Newton, a partir de su teoría de la gravedad, fue anterior al de Leibniz, pero el retraso en su publicación aún provoca disputas sobre quién fue el primero. Sin embargo, terminó por adoptarse la notación de Leibniz.

¿Que es el calculo?

Bueno nos dice que se define, rama de las matemáticas que se ocupa del estudio de los incrementos en las variables, de igual manera de  pendientes de curvas, valores máximo y mínimo de funciones y de la determinación de longitudes, áreas y volúmenes. Su uso es muy extenso, sobre todo en ciencias e ingeniería, siempre que haya cantidades que varíen de forma continua.

Introducción

Bueno breve mente se hablara del cálculo integral y diferencial, bueno una pequeña introducción de lo que es el calculo, sus antecedentes históricos, ¿Quiénes fueron sus matemáticos?, ¿que aportaciones dieron, y para que nos sirve en la vida cotidiana el calculo?, y ¿porque es importante  saber todo esto, y conque finalidad?